Lady Esmerelda's Crystal Ball

Claim:   Amazing on-line psychic trick can read minds and identify which symbol a user selected from a list of many choices.

FALSE

Origins:   An online parlor trick called "Lady Esmerelda's Crystal Ball" has been befuddling countless netizens who have been left mystified by its uncanny ability to always identify which one symbol they have chosen from a list of many different symbols. Some members of the online community have felt unsettled by the apparent proof that something lurking on the Internet could access their thoughts or that through some form of magic or witchcraft, evil-intentioned folks were capable of using their systems against them. Magic seemed to be afoot, and that deeply troubled many. So, after receiving hundreds of messages from readers who were left suspecting their computers and Internet connections of dark doings, we've chosen to write about this leg-pull even though it's merely an old magician's trick updated to appeal to a cyber audience.

It is a trick, of course; "magic" only in the sense that it's an act of misdirection, a skill that is part of every successful magician's repertoire. This is magic of the rabbit-and-hat variety, not of the broomstick-and-cauldron ilk. The key to this trick is the concept of 'forcing'

a result — that is, the magician appears to give the participant a wide array of choices from which to select, thereby amazing his audience when he correctly identifies which one of the myriad of proffered options the participant selected. The trick is that the participant hasn't really been offered a variety of choices; he's been set up through a form of misdirection to think he's choosing one of many options when he really isn't. A simple example would be a magician's asking a participant to pick a card from a deck of 52 cards, all of which are the four of clubs — if the participant believes he plucked his selection from a standard deck of cards, he'll be astounded when the magician correctly identifies his choice as the four of clubs. But it really wasn't amazing at all, because the participant couldn't possibly have selected anything other than the four of clubs.

A similar type of forced result is at work here, where the user is asked to select a two-digit number, add its digits together, subtract that total from the original number, then find the symbol corresponding to the final result from a seemingly large chart of symbols. But why does the user have to follow the rigmarole of all these numeric steps rather than simply selecting a symbol from the chart himself? The answer is that the rigmarole is necessary to 'force' the user to select a particular symbol while creating the illusion that he's freely picking one from a large list.

How does it work? In our base ten numbering system, the first digit of a two-digit number represents the number of tens, and the second digit represents the number of ones. For example, the number written as '46' is four tens plus six ones, or (4 * 10) + (6 * 1) = 40 + 6 = 46. One way to express that concept symbolically without using specific values is to say that any number written as 'XY' represents (X * 10) + (Y * 1) = 10X + Y. Likewise, when the digits of a two-digit number are added together (e.g., adding the digits of the number 46 yields (4 + 6) = 10), the operation being performed can be represented symbolically as (X + Y). So, when we choose a two-digit number, then add its digits together and subtract the results from the original number, the operation we're performing is:

(10X + Y) - (X + Y) = 9X

The key here is that although the number the user chooses (represented by X) is variable, the end result is always a multiple of nine: if X is 1, our result is 9; if X is 2, our result is 18, if X is three, our result is 27, etc. Looking carefully at the psychic trick's chart of numbers and symbols, we find that every multiple of nine possible as a result of our operation (9, 18, 27, 36, 45, 54, 63, 72, 81) is represented by the same symbol!

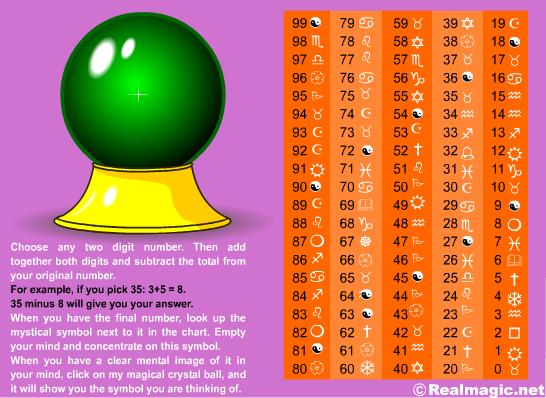
No matter which number we select initially, the numeric manipulations 'force' us into picking a symbol corresponding to a multiple of nine. And since all the multiples of nine are represented by the same symbol, we're likewise 'forced' into selecting one specific symbol — the symbol that the crystal ball 'magically' identifies as ours. The table of symbols changes each time we invoke the program, but the same symbol is always used for every multiple of nine, thereby 'forcing' the result.

Last updated:   22 September 2014